En análisis numérico, el método de Newton (conocido también como el método de Newton-Raphson o el método de Newton-Fourier) es un algoritmo eficiente para encontrar aproximaciones de los ceros o raíces de una función real. También puede ser usado para encontrar el máximo o mínimo de una función, encontrando los ceros de su primera derivada.
Descripción del método
El método de Newton-Raphson es un método abierto, en el sentido de que no está garantizada su convergencia global. La única manera de alcanzar la convergencia es seleccionar un valor inicial lo suficientemente cercano a la raíz buscada. Así, se ha de comenzar la iteración con un valor razonablemente cercano al cero (denominado punto de arranque o valor supuesto). La relativa cercanía del punto inicial a la raíz depende mucho de la naturaleza de la propia función; si ésta presenta múltiples puntos de inflexión o pendientes grandes en el entorno de la raíz, entonces las probabilidades de que el algoritmo diverja aumentan, lo cual exige seleccionar un valor supuesto cercano a la raíz. Una vez que se ha hecho esto, el método linealiza la función por la recta tangente en ese valor supuesto. La abscisa en el origen de dicha recta será, según el método, una mejor aproximación de la raíz que el valor anterior. Se realizarán sucesivas iteraciones hasta que el método haya convergido lo suficiente.
Sea f: [a, b] -> R función derivable definida en el intervalo real [a, b]. Empezamos con un valor inicial x0 y definimos para cada número natural n
Donde f ' denota la derivada de f.
Nótese que el método descrito es de aplicación exclusiva para funciones de una sola variable con forma analítica o implícita conocible. Existen variantes del método aplicables a sistemas discretos que permiten estimar las raíces de la tendencia, así como algoritmos que extienden el método de Newton a sistemas multivariables, sistemas de ecuaciones, etc.
PARA OBTENER UNA SOLUCION A F(X) = 0 DADA LA FUNCION DIFERENCIABLE F Y UNA APROXIMACION INICIAL P 0
ENTRADA APROXIAMCION INICIAL P0 : TOLERANCIA TOL: NUMERO MAXIMO DE INTERACIONES
SALIDA SOLUCION APROXIMADA P 0 MENSAJE DE FRACASO
ALGORITMO
Paso 1 tome I=1;
Paso 2 i<)= no haga paso 3-6
paso 3 tome P = P0 - F(P0) / F'(P0)
(CALCULE PI)
Paso 4 Si I p - p0 I < TOL entonces
salida (p) : ( procedimiento terminada satisfactoriamente )
parar
paso 5 tome i = i+1;
Paso 6 tome P0= P ( redefina P0)
Paso 7 salida ( el metodo fracaso despues de N0 interaccion , N0 = ' , N0);
( PROCEDIEMIRNTO TERMINADA SIN EXITO )
PARAR

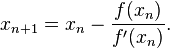
No hay comentarios:
Publicar un comentario